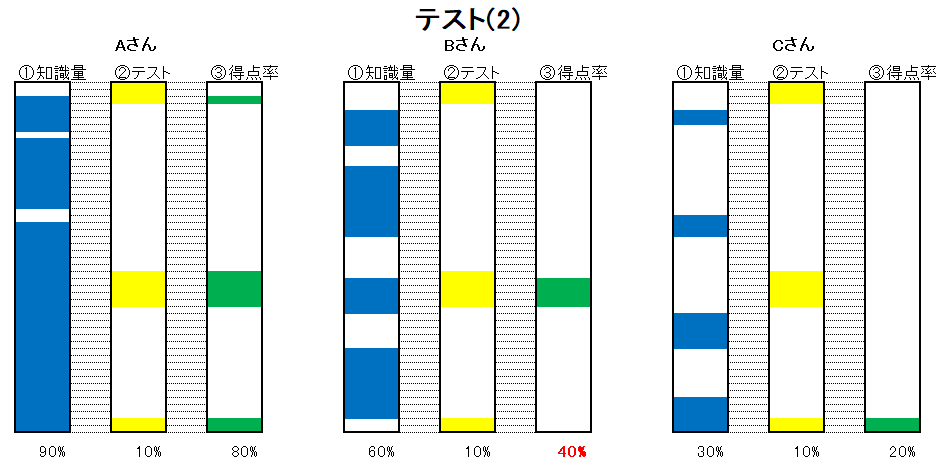
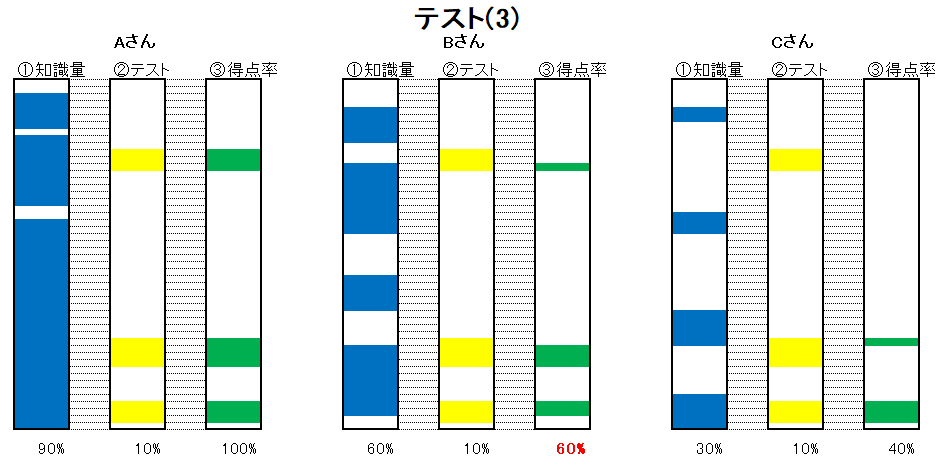
公開日 2020/07/01
7月になりました。
セミが鳴き始めましたね。
大学入学共通テストまで約29週間です。
新学期が始まってから13週間経過しました。
この意味を考え、行動を修正していきましょう。
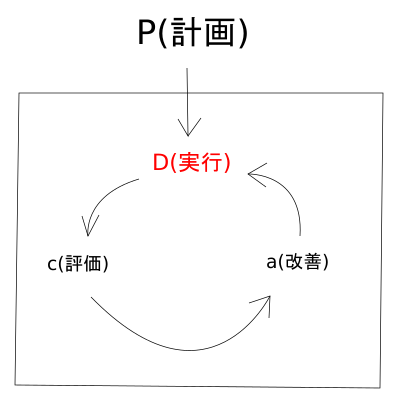
PDCAサイクルをご存知でしょうか。
仕事を効率化するための考え方です。
P…Plan(計画)
D…Do(実行)
C…Check(評価)
A…Action(改善)
これを繰り返すことによって成果を上げるんですね。
企業の新人研修などで習うこともあるみたいです。
もちろん、仕事以外でも使えます。
ただ、個人レベルではこのサイクルには欠点があると思うので、
私なりに修正してみました。
↓
名付けて、
PーDcaサイクル
です。
重きを置くのは、最初のPとDです。
例を挙げながら解説します。
まず最初に、
P…大まかな方向性を決定する。
例:志望校、学部、目標点などを決める。
つまり、最終的な目標です。
方向を見失わないために重要です。
その次からPはありません。時間の無駄です。
Dcaを繰り返していきます。
cとaが小文字であるのは理由があります。
D…とにかく、やってみる
例:問題集を解いてみる。
最も重要なフェーズです。
行動しないことには進歩はあり得ません。
人に聞く前に、まず実行。
c…成果が出たか
例:問題を解けたか。あるいは、模試の成績はどうか。
ここには時間をかけません。
Dに時間を割くためです。
Dを行う意味を問うので、Dに関係のないことは無視です。
a…Dの内容を修正
例:問題集を変える。進め方を変える。など
より効率的に成果を出すために、cに応じて変更していきます。
ここも時間をあまり割きたくないところです。
成果が出ない人は、大抵
Doが少なすぎます。
それか、Planが曖昧ですね。
分かりやすいかは分かりませんが、
ボウリングで例えてみます。
まず、投げてみます。
ピンが3本だけ倒れました。
自分が狙った方向(真ん中より少し左)に投げられませんでした。
ボールを見ていると、左に回転がかかっていました。
この原因はボールから手を放す瞬間に、手のひらがやや左を向いていることだと推測しました。
そこで次の投てきは、手に意識を集中させて投げてみました。
すると、真っすぐに投げられたものの、端のピンしか倒せませんでした。
これは、手に意識を集中して体の向きを考えていなかったからであると気づきました。
そもそも、ボールが重く身体のコントロールが不十分であるようなので、体幹を鍛えることにしました。
…
…
投げないことには、
ピンは決して倒れませんよね。
働き始めてからこれを身につけようというのは遅すぎます。
今から実践しましょう。