月: 2022年2月

公開日　2022/02/23

新年度、4月から指導方法を一部変更します。
とは言っても方針が大きく変わるわけではありません。
まずは高３生から始めます。

スケジュール管理を厳しく

これまでも特に高校生は中期目標・短期目標を設定し、
志望校合格への学習の目安を示してきましたが、
さらに目標達成率を上げるために細かい指導を行っていきます。

これまで通りの授業は行いますが、
日曜日の16時からは授業を実施せず、生徒の学習管理の時間に充てます。
具体的には、
中長期目標を前提として、

①週の学習の進捗確認
②学習到達度確認
③次週の目標(短期目標確認)

を生徒一人ずつ15〜20分程度で毎週行います。

例えば、
数学と英語の授業を受ける生徒の場合。

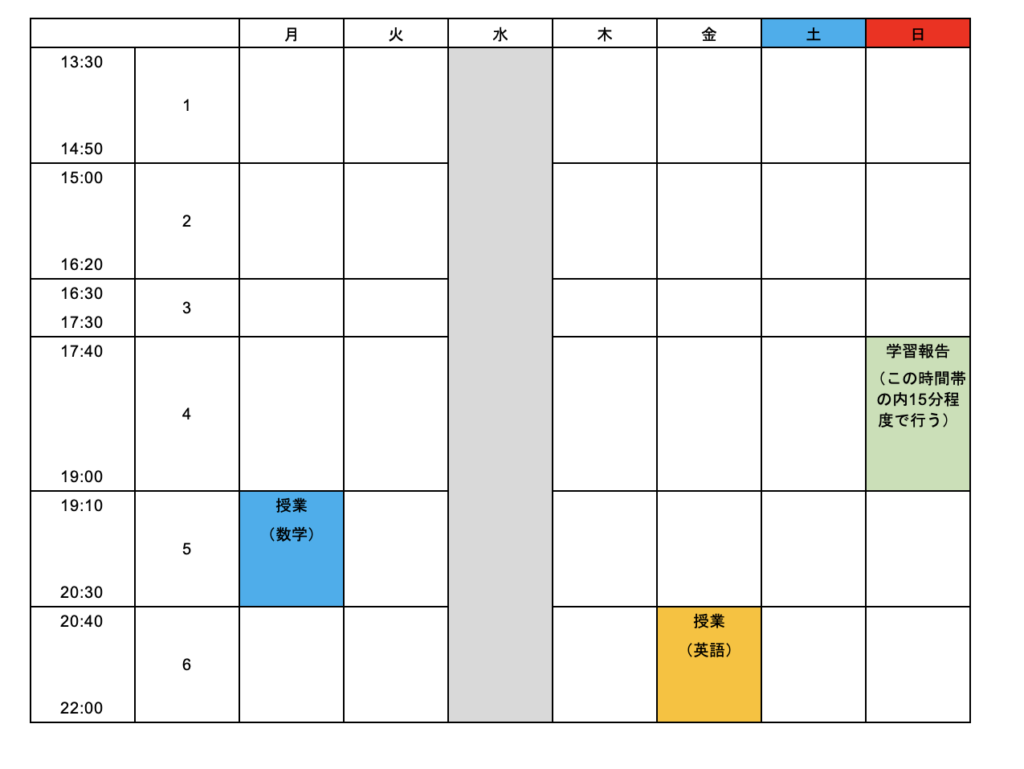
この生徒ならば、
月曜日の19:10~20:30に数学の授業
金曜日の20:40~22:00に英語の授業
日曜日の17:40~19:00の間の15分程度でその週の学習状況を報告してもらいます。
日曜日は学習報告をしたら自習をしてもらいます。

オンラインでも対応

特に、対面でのやり取りの方が良い人、
自習をするきっかけが欲しい人、家で勉強が進まない人などは
日曜日も塾へ来てもらって学習報告→自習というルーティーンを作ってもらいたいですが、
例えば送迎の都合や遠距離通学の生徒を考慮し、
学習報告だけはオンラインでも対応しようと考えています。
(会議アプリZoomを使う予定)
ちなみに、すでに自分で管理ができている生徒を特に縛るつもりはありません。

現塾生は、3月から面談を行う予定です。
(高３は全員行います。他は希望者のみ)
その場で詳しい説明を行います。

公開日　2022/02/16

中学生の進路が決まり始めました。
志望校に合格した方、おめでとうございます。
これまでよく頑張ってくれました。
楽しみな高校生活が待っていますね。
気持ちを新たにして勉強・部活その他精力的に取り組んでほしいと思います。
今回はそれを充実させるためにも、学習面でやっておくべきことを書きます。

高校の学習は中学が基礎

高校での勉強が、全く新しいことをすると考えていないでしょうか。
そうではありません。
めちゃくちゃ中学で習ったことを使います。

具体的に見てみましょう。
例えば数学Ⅱで出てくる3次関数。
$$ y=x^3-2x^2-2x+1 $$
のグラフを書け.

\(x^3\) とか見たことない！書けるわけない！と思っていませんか。
それは勉強不足です。
1次関数や2次関数のグラフを、初めどうやって書きましたか？
\(y=\frac{2}{3}x \)
このような関数のグラフを書くとき、まず点を取っていきましたよね。
\(x=3\)のとき、\(y=2\)
\(x=6\)のとき、\(y=4\)
というように通る点をとっていきます。

画像のように点をとっていき、結ぶとグラフが出来上がります。

先程の\(y=x^3-2x^2-2x+1\)のグラフは下図のようになります。

素早く書くためには、新しく微分などを理解する必要がありますが、これも直線と同じように
\(x=0\)のとき、\(y=1\)
\(x=1\)のとき、\(y=-2\)
………
とたくさん点を取っていけば絶対に書けます。
グニャグニャしてるしよくわかんない、と判断しないでください。
これがたとえ、
\(y=-x^4-2x^3-2x+5\) とか、
\(y=\frac{x^2-3x-4}{x+2}\) となったとしても同じようにできます。
全く同じようにできます。

つまり、
「代入計算してそのグラフが通る点を求めてつなげる」
ことさえ分かっていればできるということです。
このように見ていくと、
新しいことが少しずつ追加されていくに過ぎないことがわかります。

数学に限らない

関数のグラフを例に挙げましたが、
もちろん他の教科でも同様のことが言えます。
高校の勉強は、すべて中学までで習うことを基礎とします。
あなたは高校入試で満点を取ったでしょうか。
学年末テストでは？
そうではないと思います。
満点ではないということは、
まだ中学の復習が不十分なことがある、
ということです。
もちろん、満点にならないとダメということではありません。
むしろ満点を目指すことは非効率です。
ただ、中学までの基礎を徹底しておくことで、高校の勉強もかなり楽になることを覚えておき、是非高校入学までに準備をしておいてほしいと思うのです。

公開日　2022/02/09

大学入試1年前、ということで
高校2年生には現在の志望校に関して入試の科目・配点を調べてもらっています。
というのも、信じられないかもしれませんが入試1ヶ月前になっても自分が受験する試験の配点や試験時間等を知らないままの人がたまにいるからです。特にずっと親の指示にしたがってきた子など。
それではあまりに人任せですね。
自分のことをすべて他人に決められ、そのことに文句の一つもないというのであればそれでも構いませんが、そのような人はほとんどいないでしょう。

調べてきてもらうものは少しずつ集まっていますが、
みなさん調べ方があまいです。
どのような点に特に注意すべきなのかを書いておきます。

一次情報を入手する

言い換えると、
各大学HPから募集要項を調べる、ということです。
そうではなく、受験情報サイトや予備校サイトで情報を引っ張ってきている人が多いです。
そのような二次情報(ひょっとすると三次、四次情報)を引用せず、直に募集要項を読みましょう。
受験情報サイトなどが間違っていると言っているのではありません。
実際、間違いはあまりないと思います。
しかし、情報はそれが情報源から離れれば離れるほど間違っている可能性が高くなります。

小学校などでやったことがあると思いますが、伝言ゲームを思い出してみてください。
ゲームの仕切り役が各グループの一人に伝言し、グループの中でリレー形式に伝えていき、最後に聞いた人が正確に答えられるかを競うゲームです。
すべてのグループが正しく答えられたことはありましたか？
どんどん元の伝言から変わっていくこともありますよね。
噂話でも同じことが起こります。

また、例えば誤った情報を入手してしまったとして、
それが大学から直接仕入れた情報ならば大学に抗議することができますが、
それ以外の二次情報が間違っていたとしても責任は取ってくれません。
誰か(何か)を介して情報を手に入れるのではなく、自分から取りに行きましょう。
それが比較的容易にできるのがインターネットの利点です。

全て目を通す

もちろん、100ページほどある募集要項を隅から隅まで読めというわけではありません。
志望する学部学科のページだけで良いです。
何時間もかかる量ではありません。
しかしやはり皆さん読んでないです。

大学がどんな学生を望んでいるかわかりますか。
理科社会の選択すべき科目を把握しているでしょうか。
科目ごとの配点比率を理解しているでしょうか。
出題範囲は？
英検等の資格は必要ありませんか。
出願要件である大学もあります。
脚注まで全て読んでいますか。

きちんと読んでおかないと、出願資格を満たさないかもしれません。
選択すべき科目を間違えて0点になるかもしれません。
このような大事な資料を読まないのに、
社会の(どの科目もありますが)資料を読んで答える問題に正解できるでしょうか。

読んでわからない部分は誰かに訊いてください。
決して、「周りの人がしてるからなんとなく大丈夫」
などと考えないように。

公開日　2022/02/02

皆さん、勉強するときには何を使っていますか。
こう問いかけられた時に、多くの人が次のように答えると思います。

「学校の課題を解いている」
「教科書など学校教材を使っている」

一つ目の、学校の課題。
（課題を解いている）＝（勉強している）
と思っていませんか。

違います

それは学年全員共通の、与えられた課題をこなしているに過ぎません。
自分にとって必要な勉強がわかっているでしょうか。
必要な勉強は人それぞれ異なります。
英語であれば、高校生でも中学英文法から勉強する必要がある人もいれば、
医学用語の入った英文を読解する練習が必要な人もいます。
中学英文法さえ基礎がグラグラな人が、
長文読解演習をしたところで
効果はゼロに近いです。
必要なことは自分で考え、それの解決へ向け勉強しなければなりません。

二つ目の
「学校教材で勉強する」
はっきり言います。
教科書よりわかりやすい参考書がたくさん存在します。

誤解のないように言っておくと、
決して教科書で勉強するのが悪いという意味ではありません。
むしろ教科書の方が良い場面もあります。
教科書で十分と言う人もいます。

しかし考えてみましょう。
教科書よりわかりにくい参考書があったとして、
誰がわざわざそんなものを買うだろうか？
教科書では実現できないことをできるのが、書店で売られている参考書です。

というわけで、
自分で勉強する時に非常に役に立つと私が思う高校参考書をいくつか紹介します。

数学

特に個人間で差が出やすい数学。
教科書ではなかなか理解が進まない人向けに、
『初めから始める数学』シリーズ

途中計算の過程などが非常に細かく示されており、
他の本では途中が省略されていてわからなくなるような人に適しています。
数Ⅲまであります。

英語

ロイヤル英文法

英文法の辞書です。
網羅されています。
英文法をマスターしたい人、細かいことを知りたい人、私立大学の入試問題で文法満点取りたい人などにおすすめです。
別の言い方をすれば、使い方を間違えると大変なことになります。
辞書なので基本的に全てを読むものではありません。
部分的に、何か疑問が生まれた時に解決してくれる良い辞書です。
手元にあると便利ということです。
そこそこ学力のある人で、いちいち細かいことを全て解決しようとしてしまう人は特に注意。
まずは基本的な項目から覚えていきましょう。
Evergreenなどでも十分です。

物理

宇宙一わかりやすい高校物理

見た目は本当に大丈夫か、という印象ですが、
中身が素晴らしくわかりやすいです。
物理は特に教科書よりもこのような参考書をおすすめします。
こちらは問題もついていますが講義書です。
問題演習は学校で配られるものでも構いません。

化学

ゼロから劇的！にわかる理論化学の授業

こちらも非常におすすめです。
読みやすいレイアウト・フォントで、
語呂合わせもあり教科書にはない良さが満載です。
無機・有機化学編もあります。
講義系なので学校で配られるセミナーなどと一緒に使うと良いです。

5冊紹介しましたが、
もちろんまだまだ良書がたくさんあります。
勉強が進まず悩んでいる方はご相談ください。
冒頭でも書いたように、
自分で必要なことを考え解決する勉強を行いましょう。