公開日 2022/02/16
中学生の進路が決まり始めました。
志望校に合格した方、おめでとうございます。
これまでよく頑張ってくれました。
楽しみな高校生活が待っていますね。
気持ちを新たにして勉強・部活その他精力的に取り組んでほしいと思います。
今回はそれを充実させるためにも、学習面でやっておくべきことを書きます。
高校の学習は中学が基礎
高校での勉強が、全く新しいことをすると考えていないでしょうか。
そうではありません。
めちゃくちゃ中学で習ったことを使います。
具体的に見てみましょう。
例えば数学Ⅱで出てくる3次関数。
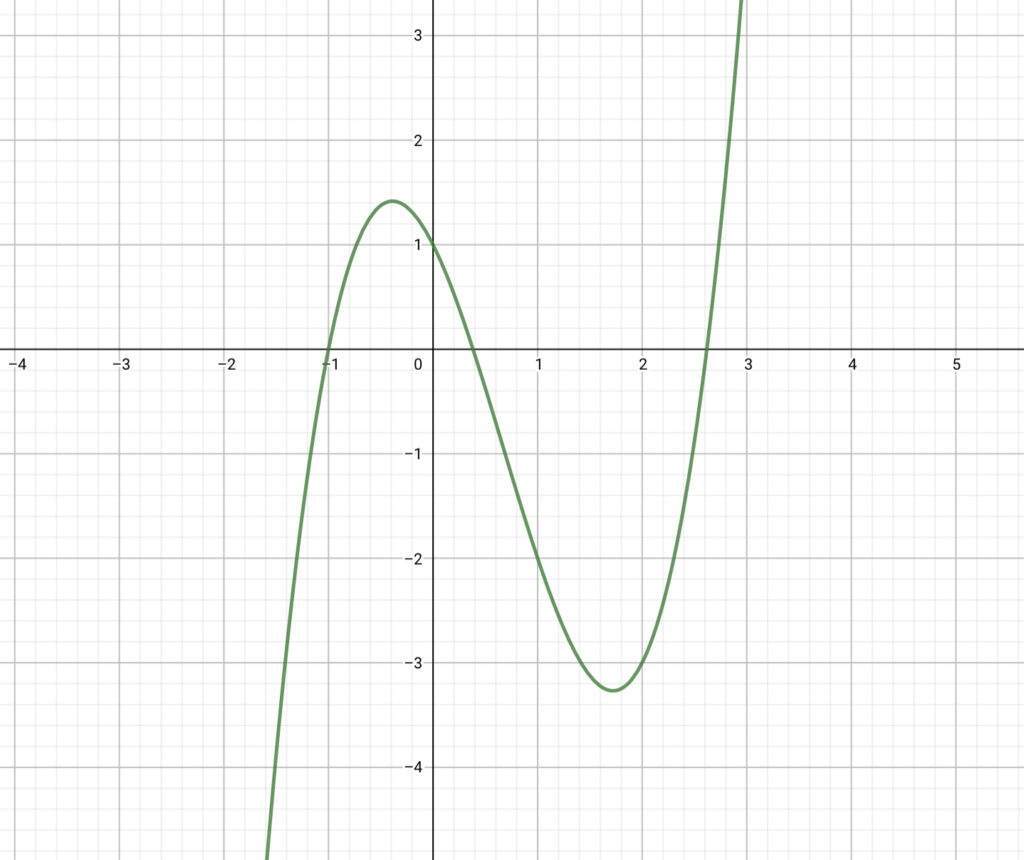
$$ y=x^3-2x^2-2x+1 $$
のグラフを書け.
\(x^3\) とか見たことない!書けるわけない!と思っていませんか。
それは勉強不足です。
1次関数や2次関数のグラフを、初めどうやって書きましたか?
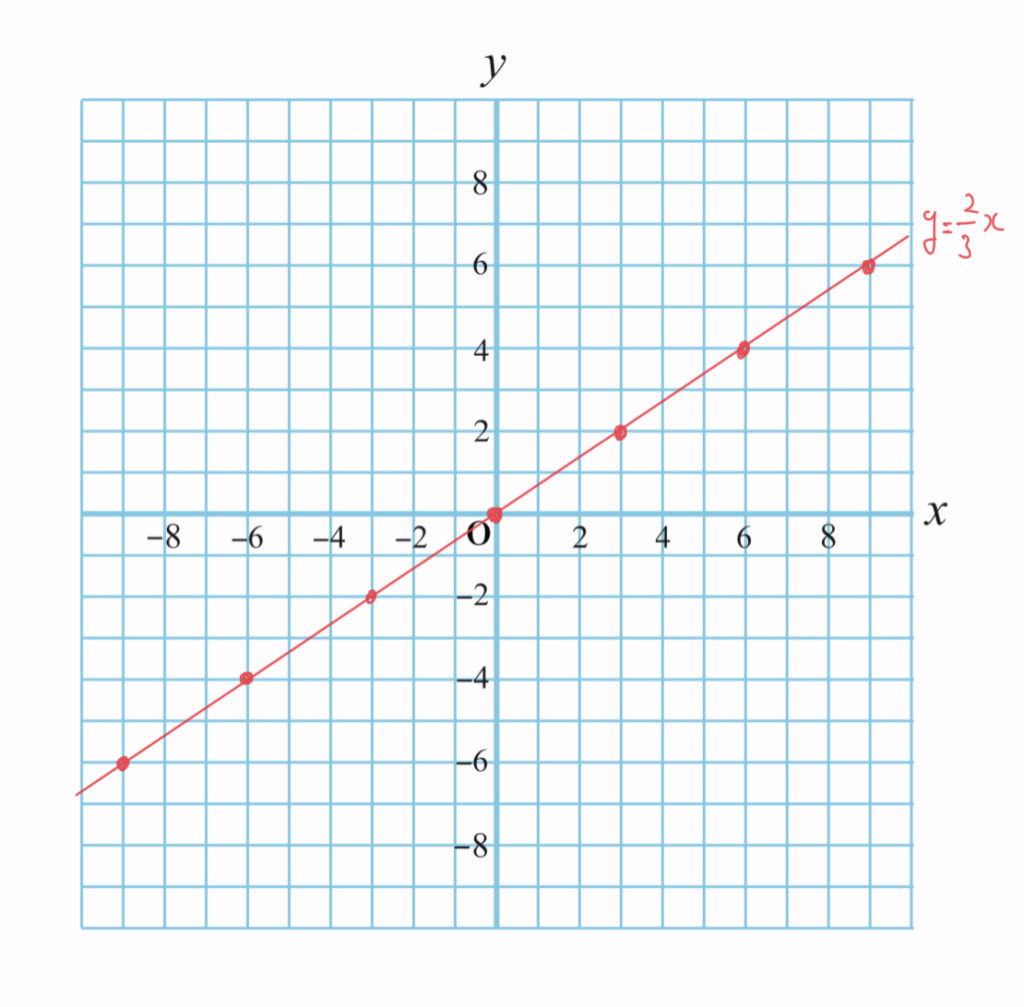
\(y=\frac{2}{3}x \)
このような関数のグラフを書くとき、まず点を取っていきましたよね。
\(x=3\)のとき、\(y=2\)
\(x=6\)のとき、\(y=4\)
というように通る点をとっていきます。
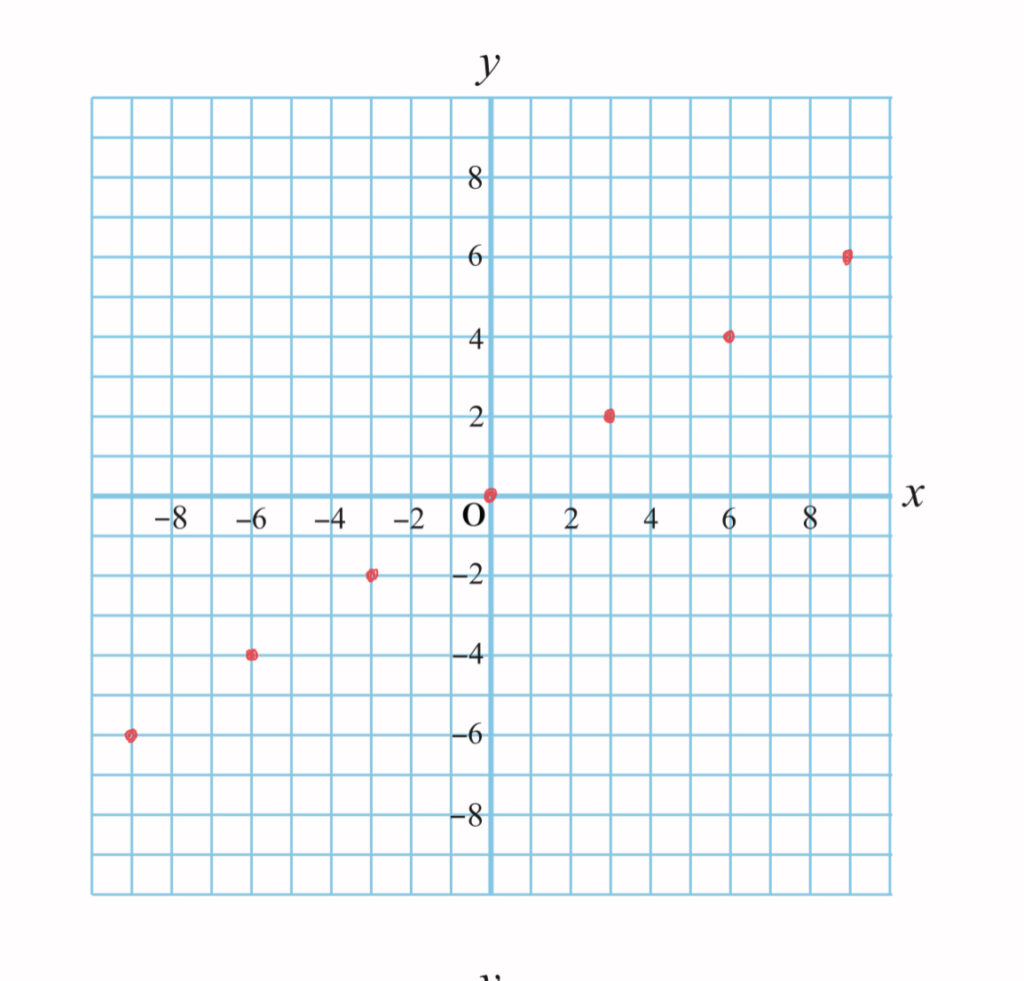
画像のように点をとっていき、結ぶとグラフが出来上がります。
先程の\(y=x^3-2x^2-2x+1\)のグラフは下図のようになります。
素早く書くためには、新しく微分などを理解する必要がありますが、これも直線と同じように
\(x=0\)のとき、\(y=1\)
\(x=1\)のとき、\(y=-2\)
………
とたくさん点を取っていけば絶対に書けます。
グニャグニャしてるしよくわかんない、と判断しないでください。
これがたとえ、
\(y=-x^4-2x^3-2x+5\) とか、
\(y=\frac{x^2-3x-4}{x+2}\) となったとしても同じようにできます。
全く同じようにできます。
つまり、
「代入計算してそのグラフが通る点を求めてつなげる」
ことさえ分かっていればできるということです。
このように見ていくと、
新しいことが少しずつ追加されていくに過ぎないことがわかります。
数学に限らない
関数のグラフを例に挙げましたが、
もちろん他の教科でも同様のことが言えます。
高校の勉強は、すべて中学までで習うことを基礎とします。
あなたは高校入試で満点を取ったでしょうか。
学年末テストでは?
そうではないと思います。
満点ではないということは、
まだ中学の復習が不十分なことがある、
ということです。
もちろん、満点にならないとダメということではありません。
むしろ満点を目指すことは非効率です。
ただ、中学までの基礎を徹底しておくことで、高校の勉強もかなり楽になることを覚えておき、是非高校入学までに準備をしておいてほしいと思うのです。