公開日 2022/05/25
数学という科目は最も個人差の出やすい科目です。
ある人は教科書を読むだけで章末の問題が解ければ、
ある人は何度説明を受けてもちょっと問題文が変わるとわからなくなります。
なぜそのようなことがあるのか。
要因は一つではありませんが、大きなものを説明します。
「同じ」とみなす
「同じ」というのは人によって認識に差があります。
例えばこれ。

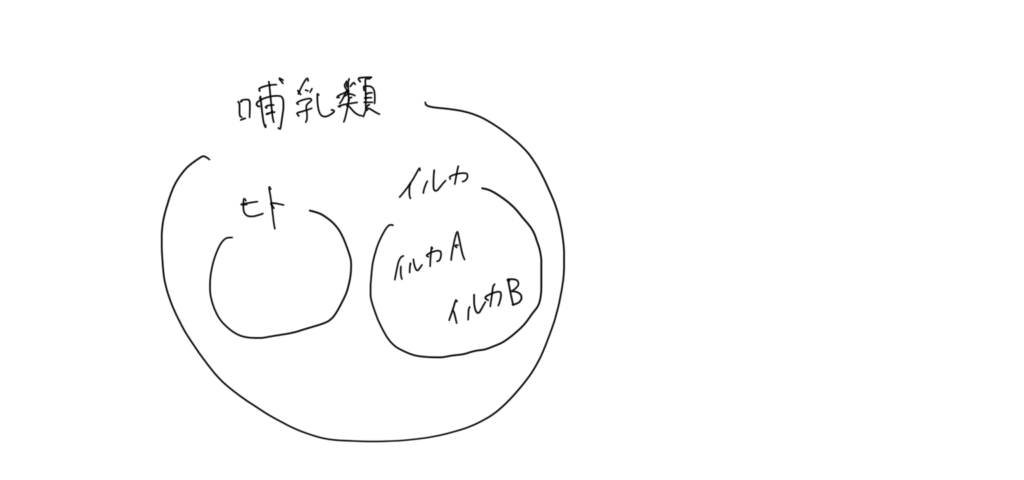
この二匹のイルカは、「個体」という目線では「違う」個体です。
背びれの形や模様なども違います。
人もそうですね。
しかし目線を上げて「種」として見ると、
バンドウイルカという「同じ」種になります。
さらに
イルカもヒトも、哺乳類という点では「同じ」になります。
これを図にすると下のようになります。
または下のようにも書けます。
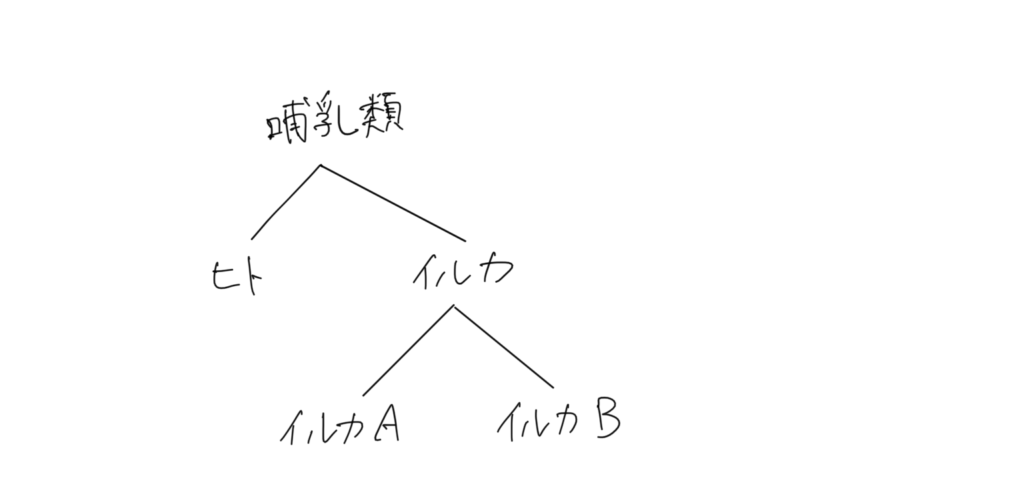
このように、どのレベルの目線で見るかによって「同じ」か「違う」かは異なります。
大きな括り(上の図では外側、下の図では上の方)は抽象化を意味します。
ヒトやイルカなどが乳で子を育てるという共通点を抽出し、哺乳類と名づけています。
このように共通点を見出す抽象化が、学習する上で非常に重要な要素になります。
なぜ重要かをもう少し詳しく書きましょう。
高校数学で習う公式の一部を挙げます。
$$y=m(x-a)+b$$
$$y=a(x-p)^2 +q$$
$$(x-a)^2 + (y-b)^2 = r^2$$
数学が得意な人はこれらを「同じ」とみなします。
逆に苦手な人はこれらは関係のない「違う」ものとして捉えます。
この3つの公式の共通点は、平行移動です。
どれも次の説明で片付きます。
すなわち、関数f(x,y)=0 をx軸方向にp、y軸方向にq平行移動すると f(x-p,y-q)=0 となる。
以上です。
解説は書きません。
これが抽象化の例です。
とにかく今伝えたいのは、この1文が分かれば3つの公式を一つ一つ違うものとして捉える必要がなく、大して覚えることがない、ということです。
逆に言うと、
これを理解しないままでいるとそれこそ公式の「丸暗記」に終わり、覚えることが多いと感じ、すぐに忘れてしまうのです。
つまり、数学がいつまでたっても理解できない人はこの抽象化を行っていません。
中学数学からのつながりに気づいていない人も多いと思います。
高校数学には2次関数、三角関数、指数関数などありますが、すべては中学の比例・反比例や1次関数からつながっています。言うなれば、中学からずっと同じことを繰り返しているのです。
抽象化はヒトにしかできない
この抽象化というのは高度な技です。
$$x = 3$$
と書いてxと3は等しい、と言っても、
「xはxであって3とは等しいはずがない」のが普通の感覚です。
動物にはこれが理解できませんし(たぶん)、理解できないヒトがいるのも当然のことです。
ゆえにあまりに理解できない場合は数学から離れて他の得意なことを見つけるのも大事です。