月: 2022年10月

公開日　2022/10/26

今回は数学の話です。
高校生の皆さん、解答解説は使っていますか。

この質問に対してはほとんどの人がYesと答えるでしょう。
きちんと使えているかどうかは別として、
今回は特に、

✅解答を読んでもすぐに忘れてしまう
✅解答を読んでもよく分からない
✅解答に書いてある答案と同じものが書ける気がしない

という悩みのある生徒へ向けた記事です。

解答と同じものが書けなくても良い

まず、「解答が唯一常に正しい」という呪縛から自らを解放させましょう。
確かに、解答解説に書いてあることは正しいことではあります。
（たまーに間違いもありますが）
ですが、全くその通りに書かないと正解にならない、というわけではありません。

例えば、中学校では三角形の合同条件の一つとして
「２組の辺とその間の角がそれぞれ等しい」
と習いますが、
定期テストでは、この合同条件と一字一句合っていないと正解としない学校があるようです。
「２組の辺とそれに挟まれた角がそれぞれ等しい」などと書くと❌ということです。

こういうふうに習うと、生徒が模範解答通りに書かないと正解とされないと考えても仕方ありません。
しかしこのまま頭カッチカチのまま高校数学へ突入すると、頭を使わない丸暗記の勉強になってしまうわけです。

上の例では実際には、
「２辺挟角相等」
という表現で済ませてもなんら問題はありません。
これを教えたら皆これを使うのではないでしょうか。楽ですし。

ともかく重要なのは、
解答は相手、または第三者に伝わるものであれば多少の表現の違いは許されます。
正しい用語、日本語で書けたらそれで良いということです。
つまり、丸暗記ではなく日本語運用力が要るということです。

模範解答はキレイすぎる

例えば次のような問題があります。

\(n と n^2+2 \)がともに素数になるような自然数nの値をすべて求めよ

↓模範解答です。

すべての素数は、\(3k\)、\(3k+1\)、\(3k-1\)、と表される。
①\(n＝3k\)のとき
　このように表される素数は3のみであり、
　このとき\(n^2+2 = 11\)
②\(n＝3k \pm 1\)のとき
　\(n^2+2 = (3k \pm 1)^2+2 = 3(3k^2 \pm 2k+1)\)
　となり\(n^2+2\)は素数ではない
①、②より、\(n\)と\(n^2+2\)がともに素数となるような\(n\)は3のみである

このような解答が、高校生が使っている教材の解答に書いてあるわけですが、
実際に問題を解いた人は、
これだけしか書いていないと思うと大間違いです。
実際には下の画像のようなことを紙面または頭の中で考えています。

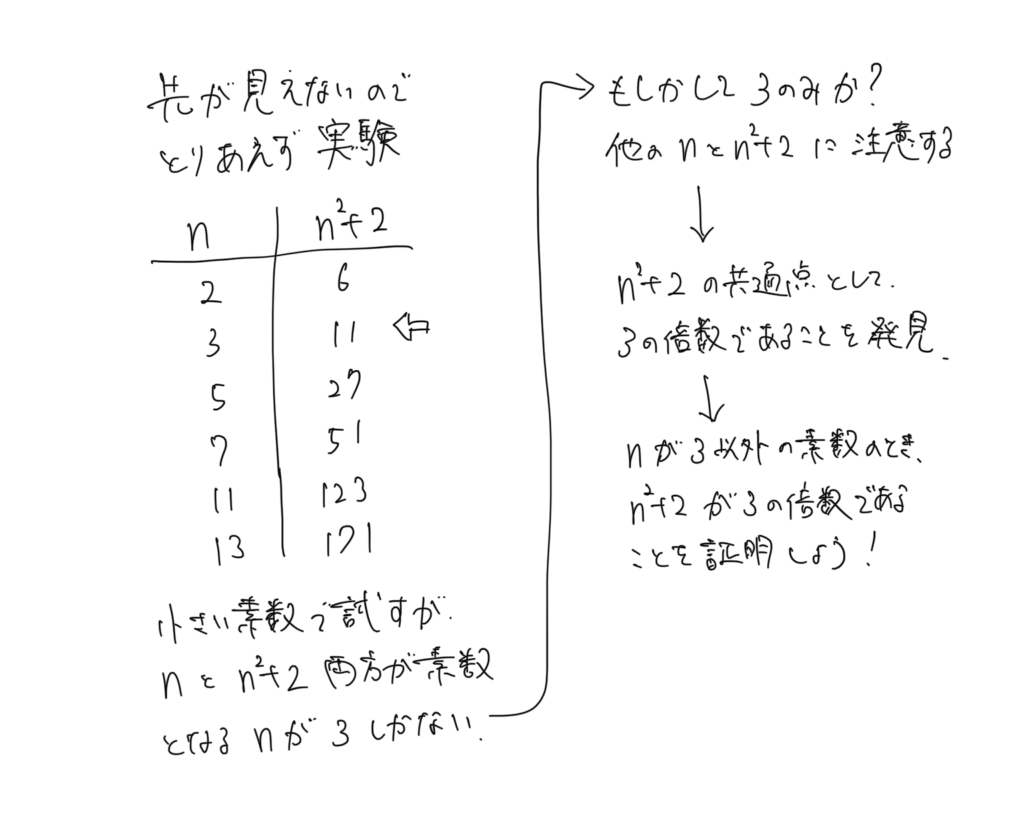
模範解答よりもこちらの方が内容が濃いと思いませんか。
これもまだ整理した方で、問題が複雑になるほど多くの試行錯誤が必要で、それを重ねた結果、模範解答のような整理整頓された答案が書かれるということを覚えておきましょう。

このような「思考過程」を全く勉強しないでいると、
それこそが無味乾燥なただの暗記になってしまうわけです。

将来役に立つ

以上のことから分かるように、
数学という科目は問題解決のためのプロセスおよびプレゼンテーションを学ぶことのできる科目であると言えます。
数学が得意ならば年収が高い傾向があるという統計がありますが、それが少しでも納得していただけるのではないでしょうか。

公開日　2022/10/19

共通テストまであと87日になりました。
今から13回目の土曜日です。
本番が近づいていたということで、高３生はそろそろ併願先を考える必要があります。
今日の記事は併願する学校選びの参考にしてください。

前提として

第一志望校に合格すること。
それが最も重要な目標ですね。
だから、併願によって第一志望校のための準備がおろそかになるようなことはできるだけ避けたいものです。

受験科目をそろえる

最も大事と言って良いのが受験科目です。
例えば国公立大学理系が第一志望の場合。
個別試験に数学、物理、化学を課すところであれば、私立大学は数学理科の２科目または３科目で受験できるところが良いです。
第一志望校が英語、数学、物理、化学の４科目だったとしても、自分の得意科目の配点が高いところがあればその方が有利に戦えます。

また、国公立大学は後期日程がありますが、小論文、面接などがある大学も多いです。
前期日程の合格発表から後期の試験日までは1週間もないと思っておいてください。
つまり、前期の合格発表で不合格を知ってからの対策はほぼ不可能であるので、前期試験の前までに準備を終えねばなりません。
前期、後期の対策を同時にする必要があるので、特に小論文は注意しましょう。
少々対策したくらいできちんと書ける人はいません。

無理のない日程で

私立大学の個別試験を受ける場合、無理のないように受験日程を組みましょう。
国公立大が第一志望の場合、共通テスト後から個別試験までの約1ヶ月間はものすごく重要な時間です。試験や受験地までの移動で疲れることもあるので、過密日程はNGです。
県外、九州外の大学でも近場で受験できる大学もあるので検討しましょう。

浪人の可能性は

最近は浪人する学生が減少傾向のようですが、浪人は悪い選択肢ではありません。
目標が明確であればする価値はあります。
志望先が限られていたり、医学部医学科のような難関ならば、強気に出ても良いのです。
その場合は併願先を絞り、第一志望校の対策に専念しましょう。
第一志望校の受験の前の練習として一校受けておくことをおすすめします。

ただし、
浪人することで作られる1年をあてにしてはいけません。
明確かつ具体的な目標がある人にだけすすめます。
そして浪人せずに志望校合格ができるよう準備ができた人のみやる価値があります。

公開日　2022/10/12

先日、本屋で参考書漁りをしていたところ、
おそらく高校生の子どもを持つ親らしき女性が店員に、
「数学の公式一覧が載っているような本はありませんか。」
というようなことを尋ねていました。
そこそこ大きな本屋で、３５歳くらいの男性店員さんは「自分はまだ参考書担当になったばかりで十分に把握してなくてすみません。」というようなことを言っていました。
私は、高校数学の公式かつ教科書に載っていない応用的な公式まで幅広く網羅されている本を教えるのか、話を聞く限りそのような公式集を持っていてもおそらく使いこなせないような学力なのでやめた方が良いと言うべきか悩んでいる間にその二人は去っていました。

公式をそのまま覚えるだけになっていないか

使い物になりません。
たとえば、三平方の定理の公式は
$$a^2 + b^2 = c^2$$
ですが、これをそのまんま文字で覚えたところで問題が解けるでしょうか。
a,b,cは直角三角形の３辺の長さで、cが斜辺であることを知っていないと使えませんよね。

他にも、
高校一年生は三角比をすでに習い、テスト範囲でもあったと思います。
三角比の定義が重要ですが、

$$sinθ = \frac{y}{r}$$

$$cosθ = \frac{x}{r}$$

などというふうにおぼえていないでしょうか。この文字のまんま。
それでは使い物になりません。
三角比の定義はわかっていません。

本当にわかっている生徒はもちろん上記のように答えることもできますが、
三角比の定義を説明してください、という問いに対してそのようには答えません。
次のような図で答えます。

これに加えて、三角比の相互関係が三平方の定理であることを説明できれば文句なしです。

公式の証明が習得の近道

証明が好きではない中学生高校生は多いですが、
証明を学習した方が、むやみに問題を解くよりも力がつきます。
なぜなら、
どのような場面でその公式を使うかがわかるからです。
公式をいつ使えば良いのかわからないという人は、その公式をただの文字列として捉えています。
公式が導かれる背景を知りません。
そもそも公式は、いつ使うのかを考えるのではなく、
必要だから使うだけです。

この２次方程式をどう解こうか？
→因数分解できないから解の公式を使おう！

ですよね。
また、証明を学習することは、
特に高校生は解答作成力に関わります。
問題に解答するには過程を書かねばなりませんが、
それ自体、自分の解答を証明するものであることに気づいてください。

公開日　2022/10/05

西九州新幹線かもめに乗ってきました。

在来線と違って座席が大きくゆったりとしているので座り心地が良いです。
武雄温泉駅で以前特急として走っていた車両に乗り換えますが、すごく小さく感じましたね。
こんなに大きなものが時速２００km以上で、ほとんど揺れずに走るのは本当にすごいなあと思います。

電光掲示板の配色は見やすいし、駅から発車後は注意していないと気づかないくらいで車内の電灯が控えめになったり、上の画像のように切符置き場があったり（使い道合ってますよね？）、いろいろと工夫されているなあという印象です。
ちなみに座席のテーブルは通称白いかもめのテーブルのデザインを引き継いでいます。
去りし時に思いを馳せる、と言ったところでしょうか。
とにかく、また乗りたいなあと思います。

本題に入ります。
これはもう定期的に書いていかねばならないと思っています。
睡眠不足の人が多い。

塾生の睡眠時間が少ないことに驚きます。
中学生が23時とか日付が変わってから寝るのは遅過ぎます。
7時に起きているようなので睡眠時間は7、8時間ですね。

短いです。
22時に寝ましょう。
そうすれば9時間。
十分な時間が確保できます。
私が小学生の時は10時間、中学生の時は9時間寝ていましたが、
学校の授業中に眠いと思ったことは片手で数えられるくらいしかありませんでした。
もちろん人によりますが、多くの人の目安になると思います。
ちなみに高校生の時はそれは6〜7時間くらいになってしまいました。
大量の課題と7:25登校のせいです。
これがなければもっと私の成績はよかったはずです。
（ごめんなさい。自己管理の甘さです。高校生の自分を殴りたい）

睡眠不足は、
特に若い人ほど注意した方が良いです。
なぜなら、自分が睡眠不足であるという自覚がしにくいからです。

若いうちは体力があるので、多少無理をしても、徹夜をしても平気という人もいると思います。
それが落とし穴です。
平気だから対して問題の無いように思えてしまうのです。
実際は脳の働きも運動能力も落ちていることに気がつかず・・・

とにかく、

日中眠くならないように寝ましょう。
まちがいなく、
パフォーマンスは上がります。

授業での理解力・集中力が上がることはもちろん、
良い睡眠が取れていると精神も安定し、つまり些細なことに動揺しなくなります。幸福感が生まれます。
運動能力が上がり、部活でも成績は上がります。
良いことづくめです。

こんなに良いことばかりなのに、
寝ることを軽視する理由があるか。
全くありません。

換気し掃除した部屋で、
自分の体に合った敷布団やマットレスに横になり、
十分な睡眠を取れば、
偏差値が５上がります。

比喩ですがそれくらい影響があります。
いっそのこと
生徒とその親御さんを対象に睡眠講座を開いてしまおうかと考えるくらいです。