公開日 2022/01/25
先に書いておきます。
今回の話は難しいです。
どれくらい難しいかというと、最難関大学を目指す人は必ず理解してほしいくらい、半分の理解度でも九大は目指せると思います。
できるだけ理解しやすいように書きますが、決して「わかりやすい」ものではないのでそのつもりで読んでいただけると幸いです。
①具体と抽象とは何か
②それらの拡張
③なぜ勉強に必要か
の順に説明します。
①具体と抽象とは
具体・・・形の見えるもの
抽象・・・物事の共通の性質を取り出したもの
例を挙げます。
具体・・・りんご、もも、みかん など
抽象・・・果物
「りんご」や「みかん」は実在する、イメージできるものですが、「果物」というもの自体はありません。
木になって果実をつけるという共通の性質を持つものをまとめて果物といいます。
②具体と抽象の拡張
「拡張」というとわかりにくいかもしれませんが、言葉の使い方を広げる、と捉えてください。
具体というのは、形の見えるものと書きましたが、必ずしも目に見えるものではありません。
また例を挙げます。
具体・・・果物、野菜、肉 など
抽象・・・食べ物
食べ物というモノがあるわけではありませんし、果物や野菜といったモノもありませんが、
果物、野菜など人が一般的に食べるものはまとめて食べ物といいます。
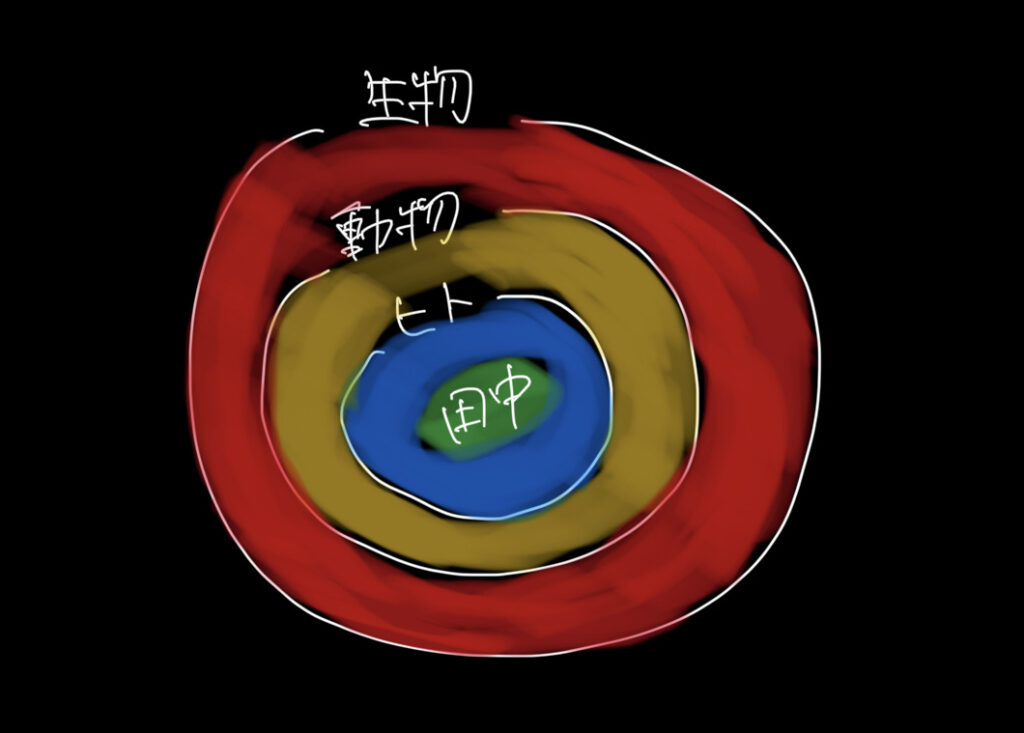
つまり、具体と抽象とは階層構造を示すものです。
次の例は、上のものほど抽象表現、下のものほど具体表現です。
生物
動物
ヒト
田中
次のように表現できます。

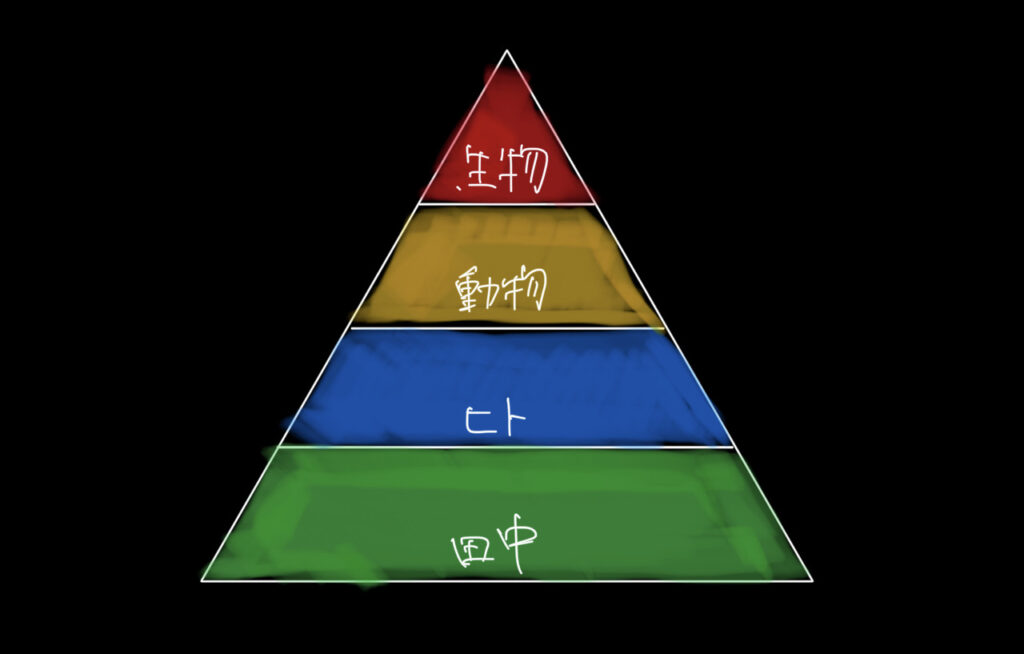
③なぜ勉強に必要か
上の三角形の図を使います。
「1を聞いて10を知る」
という言葉を見聞きしたことはありませんか。
それがこの図で説明できます。
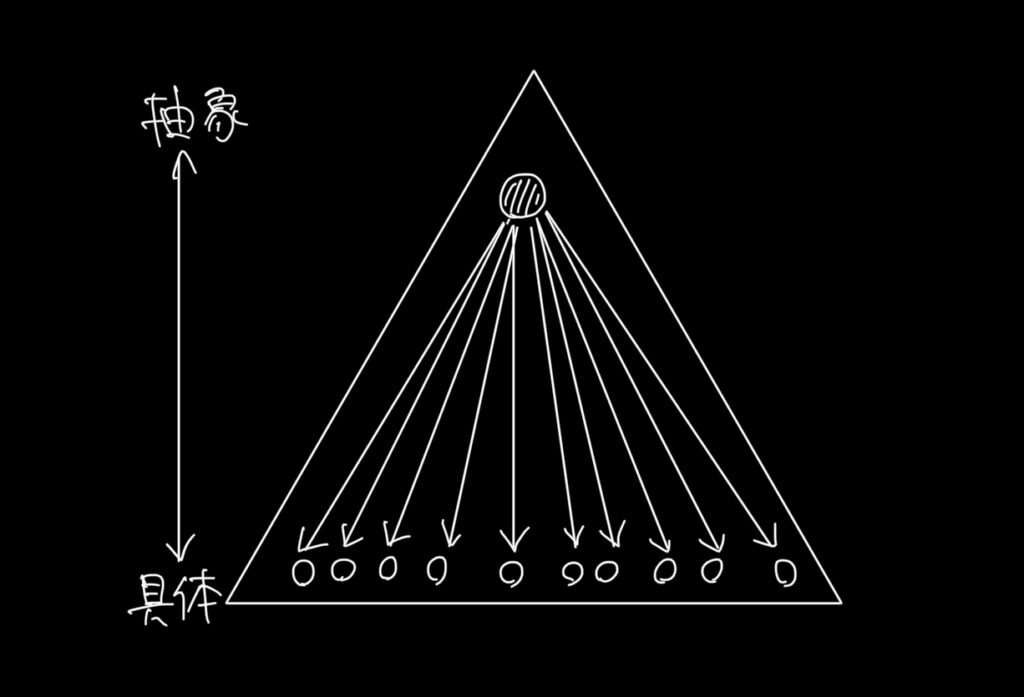
つまり、1個の抽象概念を理解できれば、10個の具体に応用できるということです。
ここでも例を挙げます。
みなさんは23×14とか137×96などの計算の結果を記憶しているでしょうか。
していませんよね。
しないといけないとすればどうでしょうか。
すごく大変ですね。
実際には、かけ算九九を暗記して、筆算のやり方を憶えて計算します。
これですね。
かけ算九九や筆算が抽象であり、それを使って計算できる23×14とか137×96が具体ということです。
計算の仕方を知っておけば、時間はかかりますが
932648594372×142739475898338
も計算できます。
これは簡単な例なので皆できますが、
勉強しても伸びない人はこの視点が欠けていることがほとんどです。
計算法を理解しない限りは、いくら問題をたくさん解いてもそれは23×14とか137×96を個別に対処していく作業にすぎず、576×373と出題されると解けなくなるのと同様に、
より抽象的な理解をしていかないと、数多く問題を解き続けてテストで全く同じ問題が出題されるのに賭けるギャンブルになってしまうのです。
そして、その抽象を理解するとは、
基礎基本を身につけることに他なりません。
ほとんどの方は逆に考えていますが、
基本が難しく、応用は(基本が理解できているという条件付きで)易しいということです。
ここまで読んで理解してくださった方は、この話が当然勉強以外にも当てはまることにお気づきのことと思います。