公開日 2025/02/05
世の中にはいろいろな数字が溢れていますが、
それを信じるか、信じないのかは自分で判断する必要があります。
数字は嘘をつきませんが、詐欺師は数字を使います。
(決して特定の人物を批判するものではありません)
数学を勉強することの大切さを少しでも理解していただけると良いと思います。
等比数列
高校数学B(だいたい高2で習う)に数列という単元があります。
例えば、
1, 3, 5, 7, 9,…
と数字を並べたものです。
この例は2ずつ増えていくので等差数列といいます。
左から順に第1項(初項)、第2項と続き、一般化して第n項を\(a_n\)と書きます。
この数列は\(a_n = 2n – 1\)と表せます。
一方、
1, 2, 4, 8, 16, …
と並べたものは等比数列といいます。
2倍を繰り返した数列ですね。この2を公比といいます。
この数列を使うと、
石破首相が打ち出した、「2020年代に最低賃金1500円」という目標がどのようなものか、理解することができます。
ところで、1万円の現金を、年利2%の銀行口座に預けると1年ごとにどうなるでしょうか?
表にしました。0.02は2%のことですね。
真ん中の列が計算式、右の列が計算後です。(小数点以下切り捨て)
| 10000 | 10000 | |
| 1年後 | \(10000×(1 + 0.02)\) | 10200 |
| 2年後 | \(10000×(1 + 0.02)^2\) | 10404 |
| 3年後 | \(10000×(1 + 0.02)^3\) | 10612 |
| … | … | |
| n年後 | \(10000×(1 + 0.02)^n\) |
つまり、n年後の預金は初項10000、公比1.02の等比数列になるということです。
10年後は、nに10を代入して12189円となります。
達成は困難?
これと同じことを最低賃金にも当てはめてみます。
厚生労働省によると、2024年の最低賃金の全国平均は1055円でした。
2029年までに1500円を達成したいとすると、年何%の増加が必要か?
まずは、2023年は1004円でしたので、1004→1055の年5%増加と仮定して計算してみましょう。
| 1055 | 1055 | |
| 2025 | \(1055×(1 + 0.05)\) | 1107 |
| 2026 | \(1055×(1 + 0.05)^2\) | 1163 |
| 2027 | \(1055×(1 + 0.05)^3\) | 1221 |
| 2028 | \(1055×(1 + 0.05)^4\) | 1282 |
| 2029 | \(1055×(1 + 0.05)^5\) | 1346 |
達成できません。
同様に、年6%で計算すると2029年に1411円。
年7%で計算すると1479円。年8%で1550円。ここでようやく達成です。
方程式ならば、
\[1055 × (1 + r)^5 = 1500 \]
を解けばよく、
\[(1 + r)^5 = \frac{1500}{1055} \]
\[1 + r = \sqrt[5]{1.42} \]
\[ r = 0.073\]
(概数計算してます)
となり、つまり年7.3%の増加で達成できると分かります。
\(\sqrt[5]{1.42}\)はiPhoneの電卓でも計算できます。
現時点での最新バージョンだと下のような画面です。
左下の電卓ボタンをタップすると出てくる、「科学計算」にするとこのようになります。
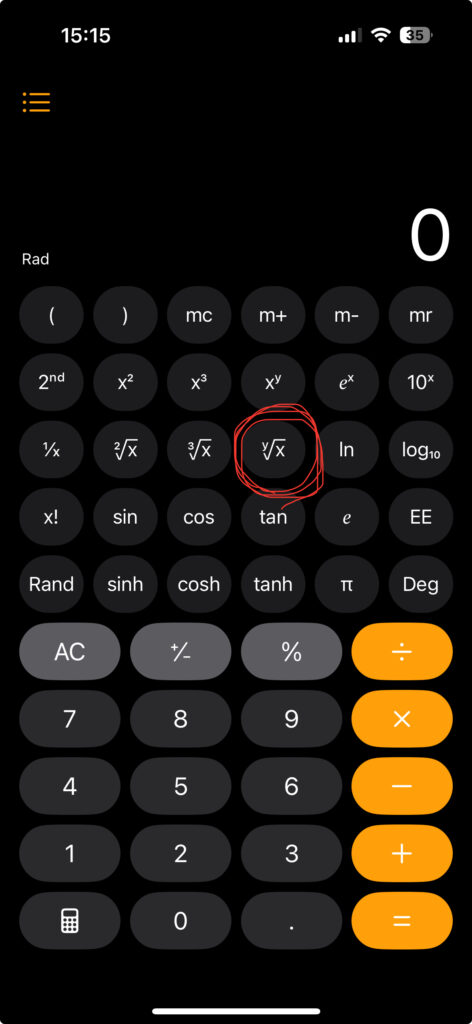
赤い丸をつけたボタンで、xのy乗根を計算できます。
ここ10年ほどを見ても、毎年の増加率は3%前後です。
→地域別最低賃金の全国加重平均額と引上げ率の推移
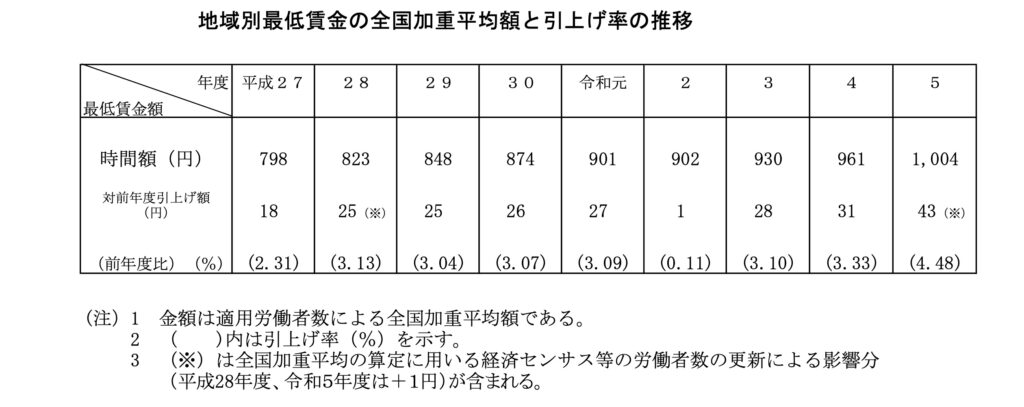
これで年7%増加と言われても…という感想の企業の方が多いのではないでしょうか。