公開日 2025/04/24
\( \triangle{\mathrm{ABC}} \)があり、\(\mathrm{AB} = 5,\mathrm{BC} = 7,\mathrm{CA} = 3, \) である。
辺\(\mathrm{AB}\)の\(\mathrm{A}\)側への延長上に\(\mathrm{AD} = 4\)となるように点\(\mathrm{D}\)をとる。\(\triangle{\mathrm{ABC}}\)の外接円と直線\(\mathrm{DC}\)との交点のうち、\(\mathrm{C}\)でない方を\(\mathrm{E}\)とする。このとき、\(\mathrm{CE}\)の長さを求めよ。
例えばこのような問題があったときに、まず何をしますか?
図形を描きますね?
次のような図を描く人が多いです。
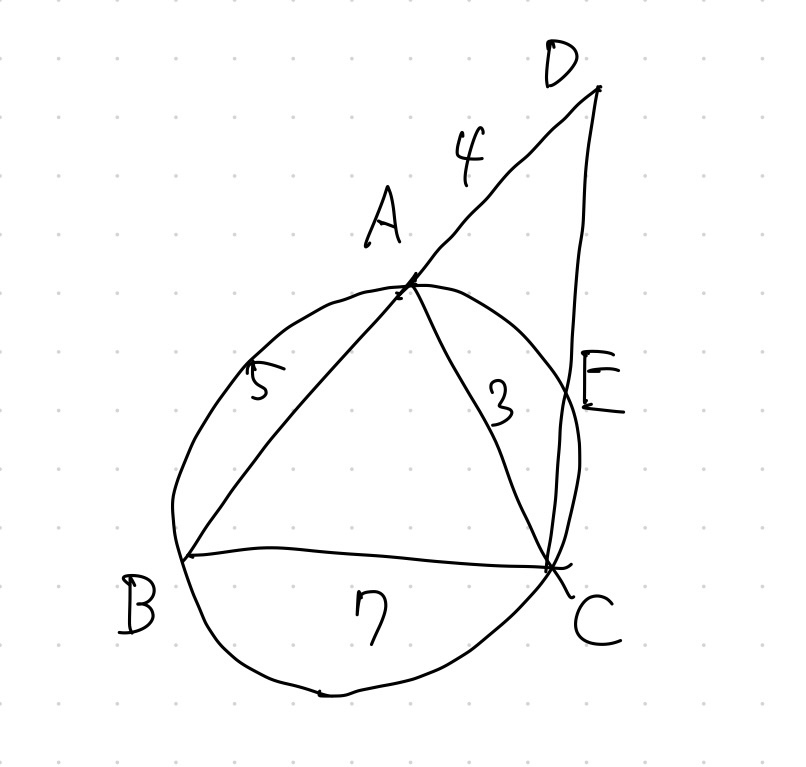
これでは、初見の問題が解けるようになりません。
初手で実力がわかる
生徒にこのような問題を解いてもらう時、特に初めの30秒を見ています。
その様子で、その問題をどれほど解き進められるかがわかります。
図形の問題ならば皆ある程度描くのですが、関数の問題になるとすぐにグラフを描き始める生徒の少ないこと。
じーっと問題を眺めていても、解法は出てきません。
図やグラフを描くという作業は、何よりも重要です。
なぜなら、
視覚化する
ということだからです。
人が取り入れる情報の大部分は視覚が占めています。
問題文に書かれている文字を読むだけでなくそれを図として出力することで、情報が生々しくなり理解が進みやすくなります。
目に見えるものの方が理解しやすいはずです。
理科で習う電流などは苦手な人が多いですね。見えないからです。
慣れてください
図やグラフを普段あまり描いてない人は、
問題に図が与えられていないと冒頭のようなものを書きがちです。
この場合、\( \angle{\mathrm{BAC}} \)は鈍角(90度より大きな角)を描く必要があります。
実際計算すると、\( \angle{\mathrm{BAC}} = 120^\circ\)です。
正しくは下図です。
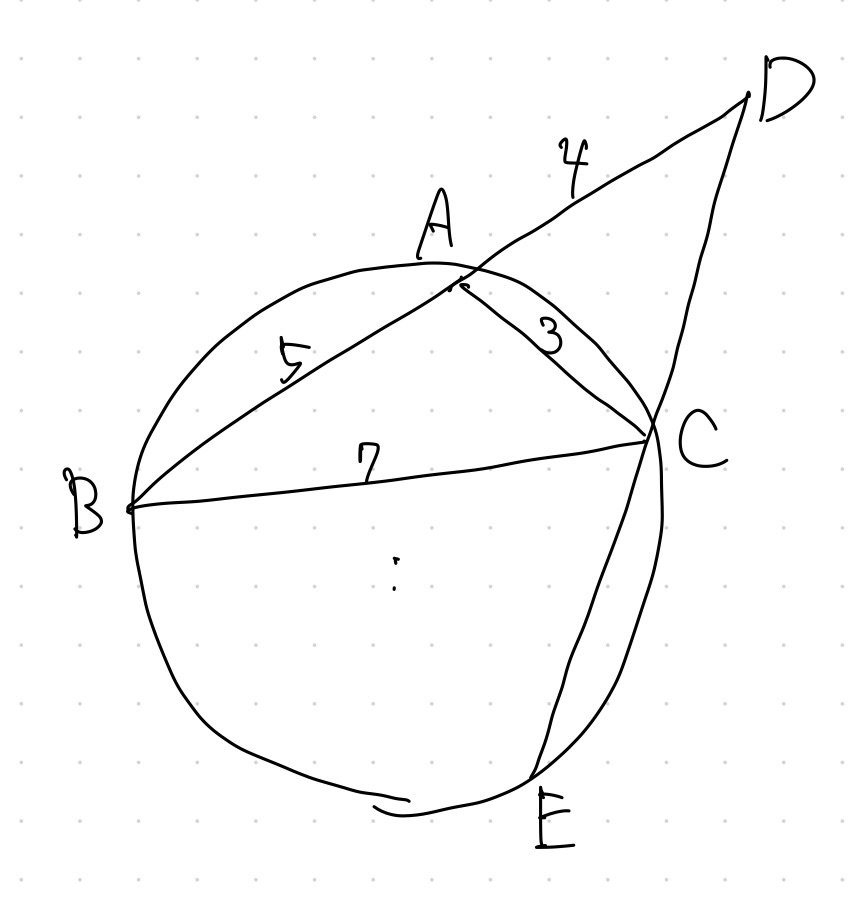
得意な人は、このような図をあっという間に描いていきます。
違いがわかりますか?
スピードだけでなく、そもそも点\(\mathrm{C}\),\(\mathrm{D}\),\(\mathrm{E}\)の位置関係が違います。
最初に描いたような図だと、その時点で正答を導くのは不可能です。
普段から描いていないとこうなります。
図を描くことの重要性がおわかりいただけるのでは。
でっかく描く
描いてもそれが小さい生徒も多いです。
図を描くことは、問題を把握するという点で最も重要。
すなわち、図が小さいということはその問題に対する理解度が低い、と言ってもよいくらいです。
自分が思っている以上にわかっていないものだと考えてください。
手を動かしましょう。