意外と知られていない偏差値に関して簡単に解説します。
数学が苦手、いや正確には数学に苦手意識を持っている方にもイメージとして理解していただけます。
簡単に言うと集団の中でどのくらいの位置にいるか、平均からどのくらい離れているかを表した数値です。(つまり相対評価です。)
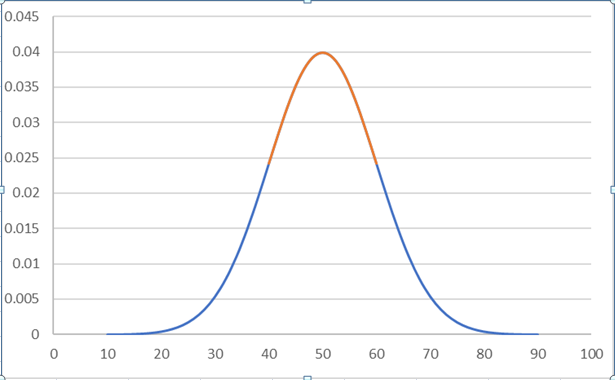
上の図で横軸は偏差値、縦軸はその偏差値の人数だと考えてください。偏差値50付近がおおよそ平均点を取っている人たちで数が多く、離れていくと数が減ります。(模擬試験ではこのような分布になることがほとんどですが、例えばほとんどの人が満点をとれるような学校の小テストや、逆にほとんどの人が解けない問題ばかりのテストでは偏差値にあまり意味はなくなります。)
偏差値40~60の間に70%弱の人が入ります。偏差値70以上は上位2%程、偏差値30以下は下位2%程です。1万人が受けた模試で偏差値60を取ると、おおよその順位は1200位です。
重要なのは、集団での位置を表す、という点です。
全く同じ試験で全く同じ点数を取ったとしても、他の人の点数によって偏差値は変わります。例えば、日本の中学生全員が受けたテストで偏差値60を取れたとしても、(同じテストで)受験したのが大学進学を目指してバリバリ勉強している人ばかりだと偏差値が40になってしまう、ということが起きます。
つまり、
テストを受けた集団のレベルが分からないと偏差値から自分の実力を正確に測ることはできない、と言えます。
これが少し怖いところです。高校生になった瞬間、やたら偏差値って使われるようになりますよね。実際のところ高1の最初の模試は、例えば諫高生だと70取れる子がざらにいます。80も取れます。これは将来大学進学をそこまで考えていない高校生もたくさん受験するからです。確か50万人弱受けます。
それが高3になると、受験人数は20万人くらいまで落ちます。絞られてきているということです。ここで偏差値70を取ることは、高1に比べるとかなり難易度が上がります。同じ名前の模試でも単純に前回と比較するのはあまりよろしくないと考えます。
イメージは持っていただけたでしょうか。数学的な話もいずれ書こうかと思います。
早く知りたい方は直接訊いてください!