公開日 2022/10/12
先日、本屋で参考書漁りをしていたところ、
おそらく高校生の子どもを持つ親らしき女性が店員に、
「数学の公式一覧が載っているような本はありませんか。」
というようなことを尋ねていました。
そこそこ大きな本屋で、35歳くらいの男性店員さんは「自分はまだ参考書担当になったばかりで十分に把握してなくてすみません。」というようなことを言っていました。
私は、高校数学の公式かつ教科書に載っていない応用的な公式まで幅広く網羅されている本を教えるのか、話を聞く限りそのような公式集を持っていてもおそらく使いこなせないような学力なのでやめた方が良いと言うべきか悩んでいる間にその二人は去っていました。
公式をそのまま覚えるだけになっていないか
使い物になりません。
たとえば、三平方の定理の公式は
$$a^2 + b^2 = c^2$$
ですが、これをそのまんま文字で覚えたところで問題が解けるでしょうか。
a,b,cは直角三角形の3辺の長さで、cが斜辺であることを知っていないと使えませんよね。
他にも、
高校一年生は三角比をすでに習い、テスト範囲でもあったと思います。
三角比の定義が重要ですが、
$$sinθ = \frac{y}{r}$$
$$cosθ = \frac{x}{r}$$
などというふうにおぼえていないでしょうか。この文字のまんま。
それでは使い物になりません。
三角比の定義はわかっていません。
本当にわかっている生徒はもちろん上記のように答えることもできますが、
三角比の定義を説明してください、という問いに対してそのようには答えません。
次のような図で答えます。
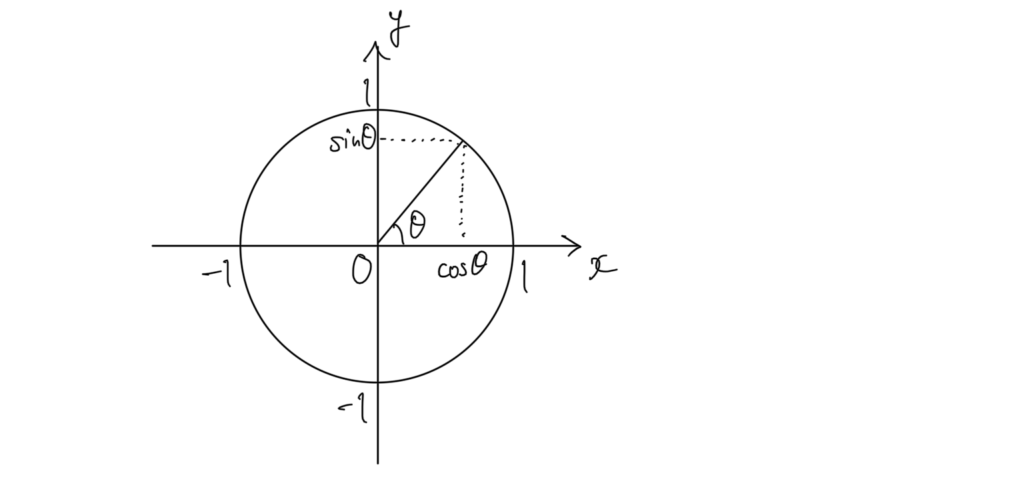
これに加えて、三角比の相互関係が三平方の定理であることを説明できれば文句なしです。
公式の証明が習得の近道
証明が好きではない中学生高校生は多いですが、
証明を学習した方が、むやみに問題を解くよりも力がつきます。
なぜなら、
どのような場面でその公式を使うかがわかるからです。
公式をいつ使えば良いのかわからないという人は、その公式をただの文字列として捉えています。
公式が導かれる背景を知りません。
そもそも公式は、いつ使うのかを考えるのではなく、
必要だから使うだけです。
この2次方程式をどう解こうか?
→因数分解できないから解の公式を使おう!
ですよね。
また、証明を学習することは、
特に高校生は解答作成力に関わります。
問題に解答するには過程を書かねばなりませんが、
それ自体、自分の解答を証明するものであることに気づいてください。