公開日 2020/04/08
緊急事態こそ、状況を客観的にとらえ、適切な判断をする必要があります。
日々学習することはこのような時にも役立ちます。
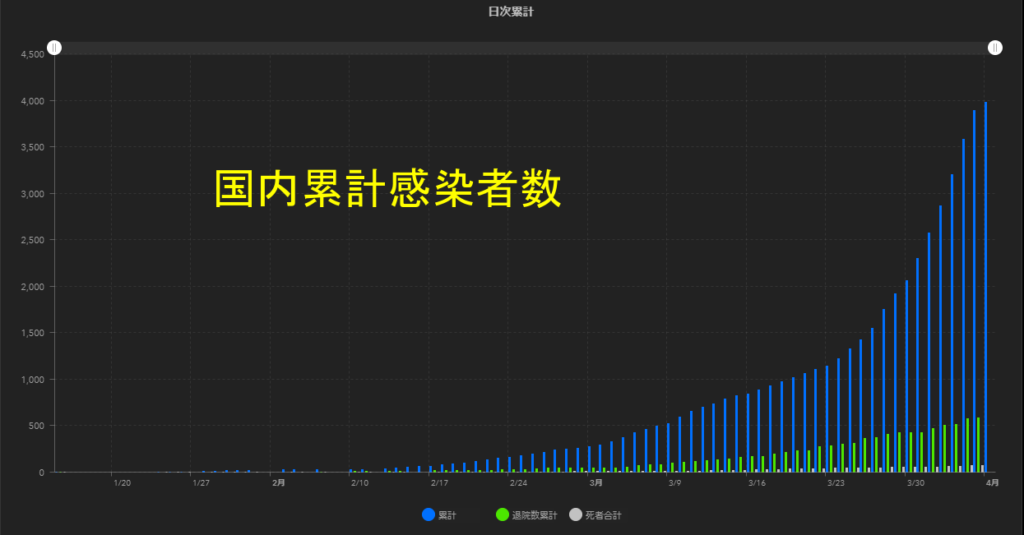
https://gis.jag-japan.com/covid19jp/ より
グラフは日本国内の累計感染者数(PCR検査陽性者数)を表しています。(青い棒グラフ)
横軸は日付、縦軸は累計数です。
感染者数が指数関数的に増加しています。
ここで、「指数関数的」とは何かを説明します。
指数関数とは
最初に一次関数です。中学生が学習します。
y=ax+b
と表されるのが一次関数です。例えば、
y=2x+3
という関数があったとして、xに代入して返ってくるyの値は下の表のようになります。

一次関数は、xの増加量に対するyの増加量は一定です。
次に、指数関数とは一般に
y=a^x
と表されるものです。
(「a^x」は、aをx回かけるということ)
例えば、y=2^x という指数関数は、xに3を代入すると、
y=2^3=2×2×2=8 となります。
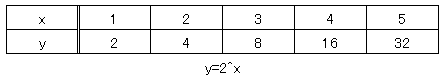
指数関数は、xの増加量に対するyの増加量がどんどん増えていきます。
例えば、1個の細胞がx回分裂するとy個になりますね。
グラフにすると下図のようになります。(横軸がx軸、縦軸がy軸)
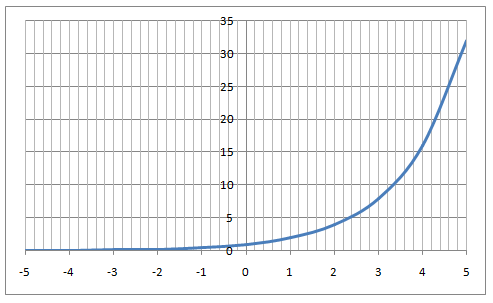
最初に出したグラフにそっくりですよね。
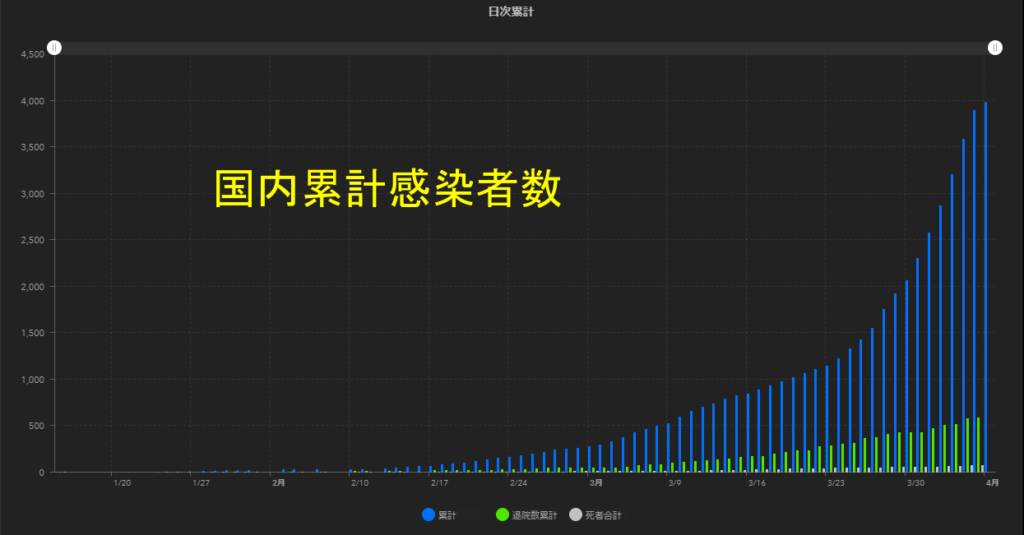
なぜこのような「指数関数的」増加の仕方をするかというと、
1人から多人数へ感染するからです。
例えば、1人の感染者が3人へうつしていけば、

このようになります。
前に出した、y=2^x よりも増加幅が大きいですね。
放っておくと膨大な数になってしまいます。
だから、早い段階で感染を防ぐ必要があります。
ちなみに、このグラフの左の方、1月あたりが見にくくなってしまっていますよね。目盛りの幅が小さくなっているからです。
これを解消して見やすくしたのが、対数目盛のグラフです。
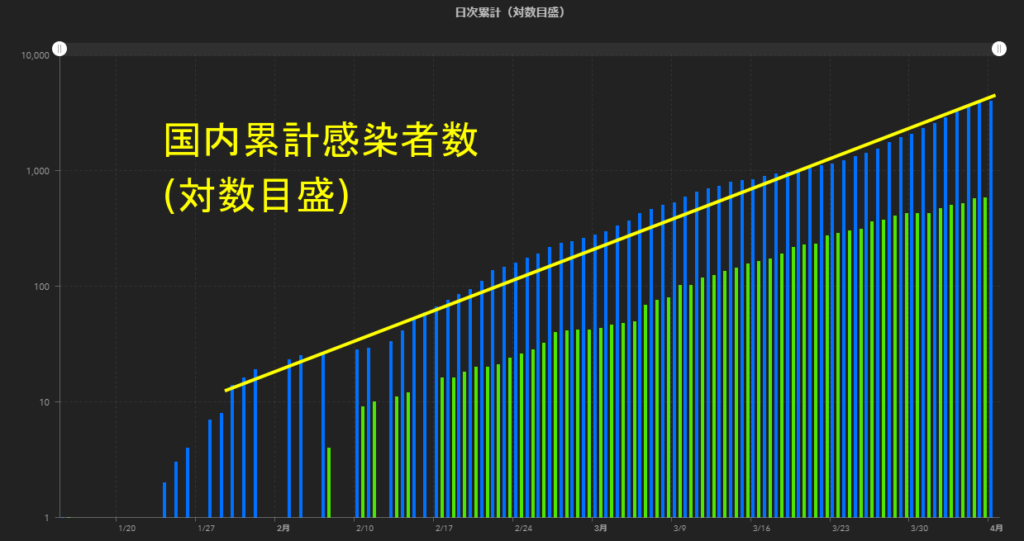
https://gis.jag-japan.com/covid19jp/ より
縦軸が10,100,1000となっています。
これで大まかな比較がしやすくなります。
また、曲線が直線になったので、将来の予想も読み取りやすくなりますね。
仮に今のままのペースで増加すれば、4/20頃に10,000人を突破します。