公開日 2021/03/10
前回、共通テストレポート①の続きです。
1日目の昼休みです。
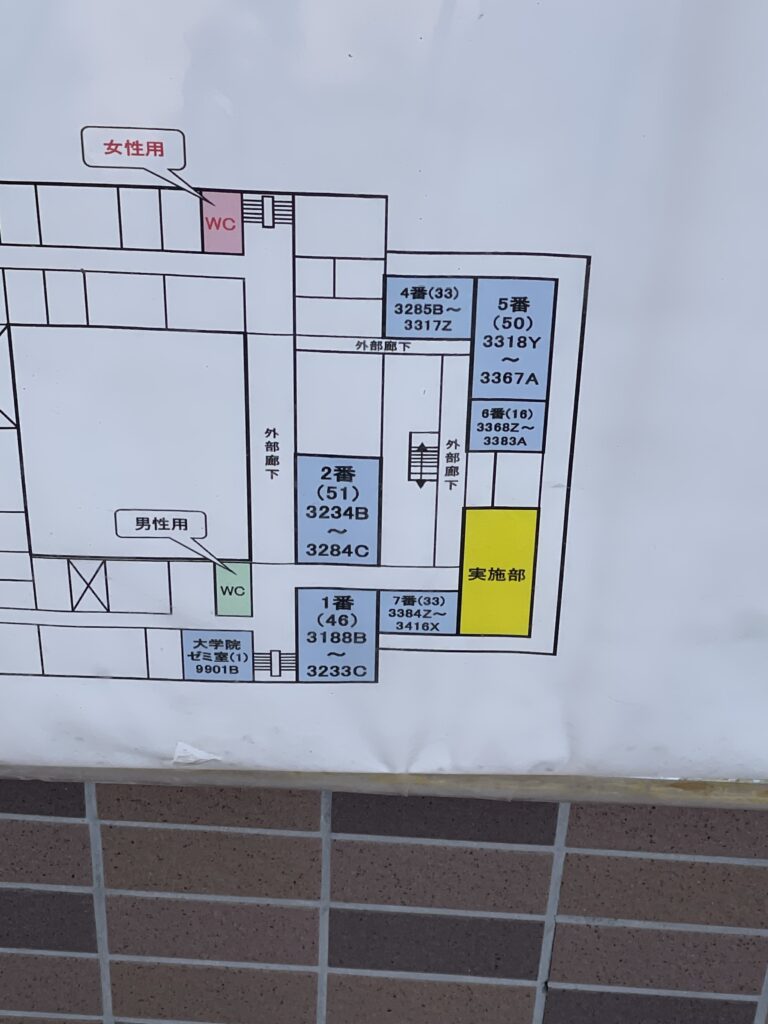
大学構内に2カ所休憩、待機用の部屋が設けられていました。


1日目はあまり存在を知られていなかったのか(?)
利用している人はほとんどいませんでした。
暖房が効いていたのでここは暖かかったです。
午後から国語、英語の試験です。
地歴公民と同様に最初に受験上の注意、説明を受けます。
リスニングですが、教室に放送を流すのではなく、
全員にICプレーヤーが配られます。
秋の模試からこれを使って練習するので心配いりません。
イヤホンが耳に合わない場合は出願時に申請しておく必要があります。
当日申し出ても対応してもらえません。
耳に合わない場合は手で抑えて聞くよう指示がありました。
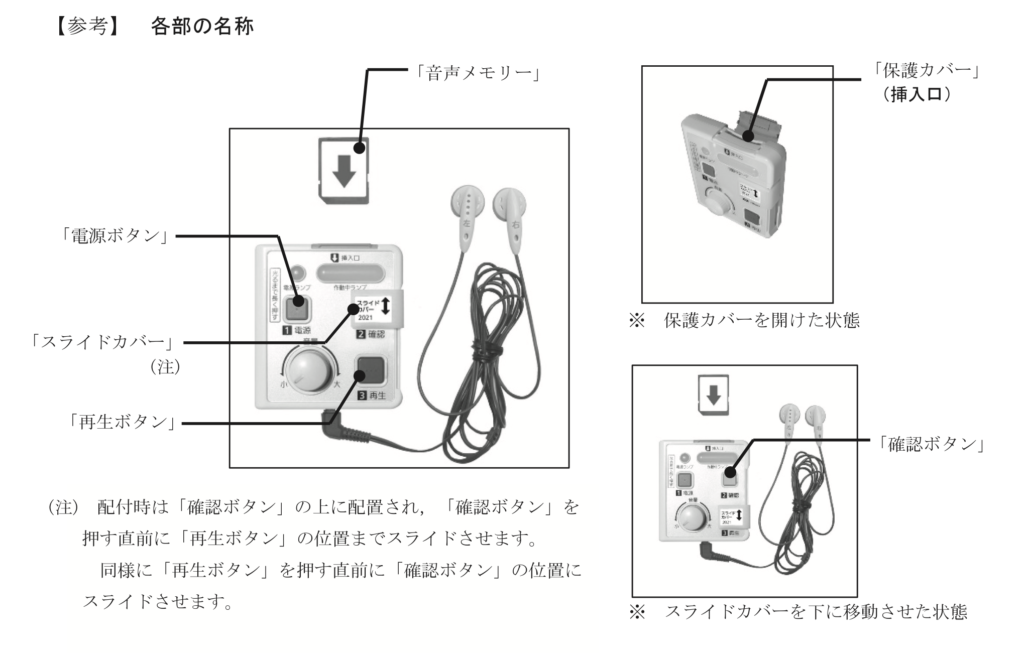 大学入試センターウェブサイトより
大学入試センターウェブサイトより
開始直前に近くを消防車が通過したので5分遅れて始まりましたが、
問題なく終了しました。
1/17(日) 試験2日目
理系科目の試験です。
理科基礎を受ける人は9:30試験開始、
数学ⅠAからの人は11:20開始です。
行動は1日目とほとんど同じです。
私の受験室の試験監督は1名交代していました。
全員変わった教室もあれば、全く同じ教室もあったそうです。
1日目にはなかったのですが、私の隣で受験していた浪人生(?)が机の上にシャープペンシルの芯のケースを置いていることをその代わった試験監督に指摘されていました。おそらく1日目の監督は気づかなかったのでしょうね。
ちなみにシャーペンの芯は置いていてもよいですがそれはおすすめしません。
それより複数のペンを置いておいた方が良いです。
扱いづらいですし、そんなに芯を使うことなんてありませんからね。

その隣にいた受験生なんですが、
2日目は少し様子が変でした。
焦り、不安なんでしょうが、少し唸ったりしてましたね。
こういうのが本番では起こるので、余裕を持って望むことが大切です。
また、今年はコロナ予防のため教室を換気する時間を長くとっていました。
休み時間中はドアや窓を開けっぱなしにしています。
防寒具必須ですね。
特に手は冷えると文字を書くスピードが落ちるのでカイロなどを準備しておくのが良いです。
2日目は特に遅れはなく終了しました。

↑受験室の一つ。私が受けた教室ではありません。
帰りはかなり混雑します。
今まで気をつけていたのは何だったんだってくらい路面電車は混んでましたね。
電車で行く人は気をつけてください。
タクシーを使うか、浦上駅までは30分程度なので歩いても良いと思います。
帰宅後自己採点を行いました。
結果はこちら↓
国語 155/200
英語R 86/100
英語L 87/100
数ⅠA 68/100
数ⅡB 100/100
地理B 73/100
現社 74/100
物理 75/100
化学 77/100
合計 721/900
合計は、国英数理2地で計算しています。
また、得点調整分は考慮していません。
数学ⅠAは、完敗ですね。本番は何が起こるか分かりません。
現社は、伊達に30年生きていないのでけっこう取れました。
模試を受けることがどれほど重要か、再認識させられましたね。
新高3は特に、毎回の模試を本番のつもりで受けてください。
また今回、いろいろな濃さの鉛筆やマークシート用シャーペンなどを実験として使用したのですが、正式な結果が帰ってきたら報告します。